Consider the moments when you tune a radio, adjust the volume, or synchronize a video with its audio. In these instances, you are actually manipulating three fundamental properties of signals: frequency, amplitude, and phase. These elements are essential to modern electronics, influencing everything from wireless communication to audio processing.
Frequency: The Speed of Signal Oscillations
Frequency refers to the number of cycles a signal completes per second and is measured in Hertz (Hz). For instance, a signal with a frequency of 1,000 Hz (or 1 kHz) completes 1,000 cycles in one second.
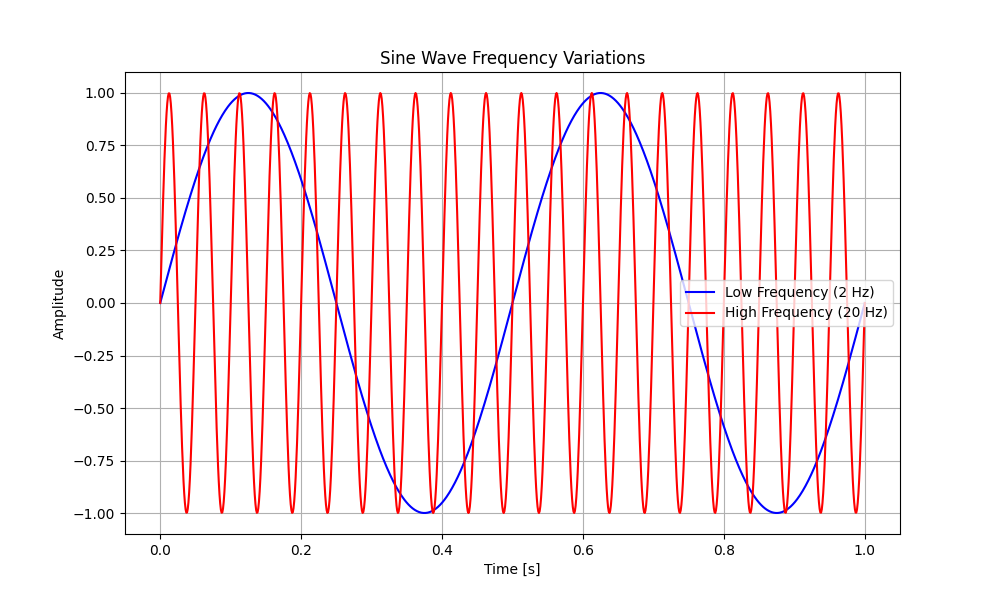
Frequency plays a pivotal role in determining various aspects of a signal, including its pitch, data transmission speed, and operating range in electronic circuits.
- Pitch of Audio Signals:
In audio signals, frequency is directly related to pitch. The higher the frequency, the higher the pitch of the sound.
For example, a sound wave with a frequency of 440 Hz corresponds to the musical note A4, which is a common reference pitch in music. Human hearing typically ranges from 20 Hz to 20,000 Hz, with frequencies below 20 Hz considered infrasonic and those above 20,000 Hz considered ultrasonic.
- Speed of Data Transmission:
In communication systems, frequency determines how quickly data can be transmitted. For digital systems, higher frequencies allow for faster transmission of information, meaning more data can be sent in a shorter amount of time.
For example, high-frequency signals are used in radio waves to carry information over long distances, and higher frequencies in wired connections (like fiber optics) enable faster internet speeds.
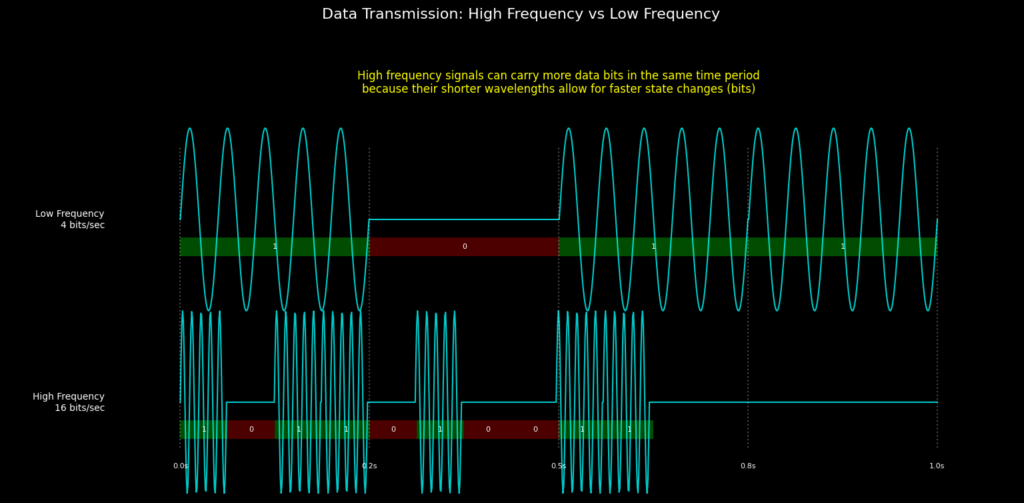
- Operating Range of Electronic Circuits:
The frequency of a signal also defines the operating range of electronic components and circuits. Certain circuits, such as filters, oscillators, and amplifiers, are designed to operate efficiently only within specific frequency ranges.
For instance, an audio amplifier typically operates in the low-frequency range (20 Hz to 20 kHz), while a radio transmitter might operate in the radio frequency (RF) range (hundreds of kHz to GHz).
Mathematical Representation
A sinusoidal signal can be represented as:
\[x(t) = A \cos(2 \pi f t + \phi)\]
where:
- \( A \) is the amplitude,
- \( f\) is the frequency,
- \( \phi \) is the phase,
- \( t \) is time.
Types of Frequency in Signal Analysis
- Low-frequency signals (0 – 1 kHz): Used in power systems and audio signals.
- Mid-frequency signals (1 kHz – 1 MHz): Found in radio communications.
- High-frequency signals (above 1 MHz): Used in microwave and RF applications.
Amplitude: The Strength of a Signal
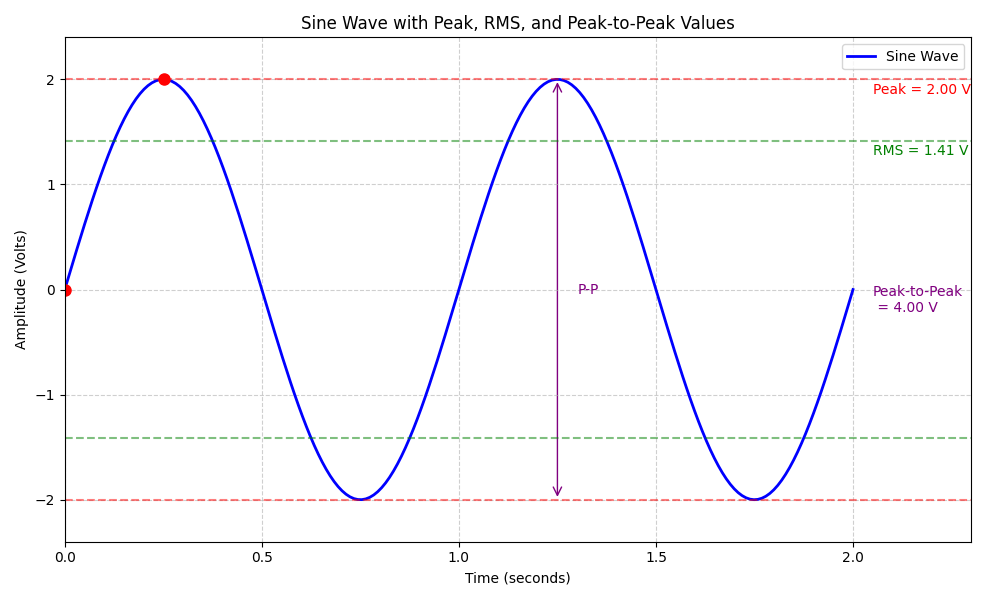
Amplitude refers to the peak value or maximum magnitude of a signal, representing how far the signal moves from its baseline (zero) during each cycle. In practical terms, it determines the signal’s strength or intensity. A higher amplitude means a stronger signal, which is crucial for ensuring reliable transmission and reception.
Amplitude affects the power levels in both analog and digital systems, which impacts how efficiently a signal is transmitted over a medium.
In communication systems, for example, a signal with insufficient amplitude may experience attenuation, leading to a loss in quality or complete signal failure (the signal basically becomes noise). Conversely, excessive amplitude may cause distortion or interference, so maintaining the right amplitude is vital for optimal signal integrity.
Mathematical Representation
Amplitude in a sinusoidal wave is the peak value:
\[ A = max(x(t))\]
Types of Amplitude Measurements
- Peak amplitude (A): The highest positive or negative value.
- Root Mean Square (RMS): The effective power of AC signals, calculated as:
\[ A_{\text{RMS}} = \frac{A}{\sqrt{2}} \text(for\ sinusoidal\ signals) \]
- Peak-to-peak (P-P): Difference between the highest and lowest points.
Phase: The Timing of a Signal
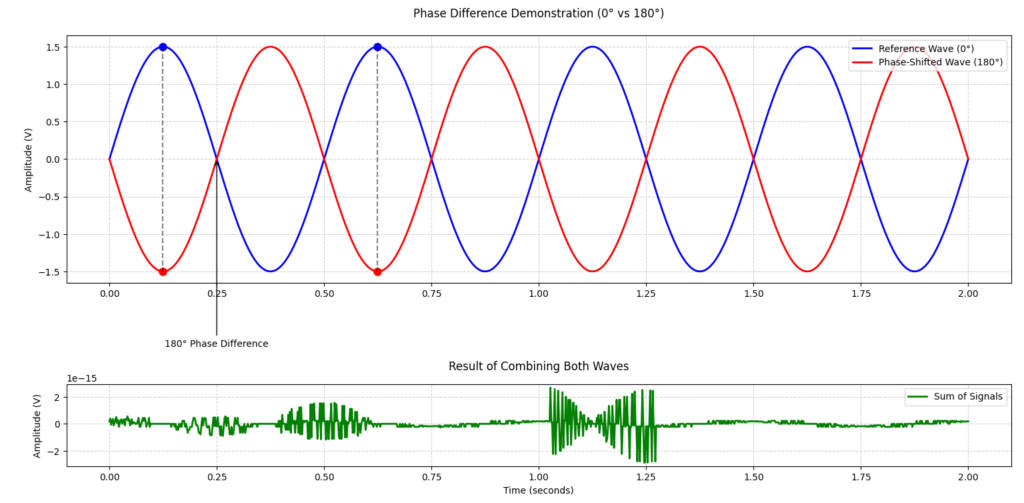
Phase refers to the specific position or timing of a waveform in its cycle relative to a reference point, typically measured in degrees or radians. A full cycle of a waveform is 360 degrees or 2π radians. Understanding phase is essential because it tells us where in the cycle the waveform is at any given moment. For example, a waveform at 0° is at its starting point, while a waveform at 180° is at its opposite peak.
In communications, phase plays a critical role in synchronization, as signals need to be aligned in time for proper transmission and reception. If two signals are out of phase, meaning they don’t match up in timing, they can interfere with each other, causing distortion or data loss. This is particularly important in systems like radio broadcasting, where multiple signals share the same frequency. The phase of each signal ensures that they can coexist without causing interference, a concept known as phase modulation.
Phase also governs signal coherence, or the degree to which multiple waveforms stay synchronized over time. When waves are coherent, their phases remain aligned, and their interaction is predictable (see figure below). Conversely, if the phases of signals shift over time, the waves become incoherent, leading to unpredictable behavior and potential signal degradation.
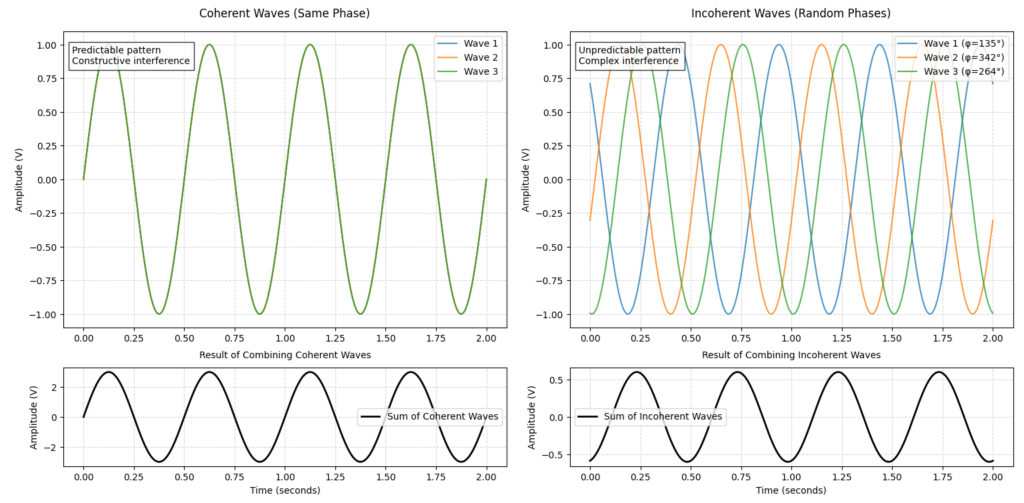
Lastly, phase affects waveform interaction. When two signals are in-phase (i.e., their cycles align), they can combine constructively, amplifying the overall signal. However, when they are out-of-phase (such as 180° apart), they can cancel each other out, a phenomenon known as destructive interference. This interplay between phase and signal strength is critical in various applications, including audio processing, RF communication, and signal filtering.
Mathematical Representation
Phase shift modifies the position of a wave:
\[x(t) = A \cos(2\pi f t + \phi) \]
Where \(\phi\) is in radians or degrees.
Types of Phase Relationships
- In-phase signals: Waves align perfectly ( phase difference).
- Out-of-phase signals: A shift occurs (e.g., means opposite polarity).
- Quadrature signals: A 90-degree phase shift is used in modulation.
Relationship Between Frequency, Amplitude, and Phase
Waveform Representation in Signal Processing
In signal analysis, frequency, amplitude, and phase are interconnected properties that define the overall behavior of a waveform. A signal is rarely a simple sine wave; instead, it is often a combination of multiple frequency components, each with its own amplitude and phase.
One of the most powerful tools for analyzing these components is Fourier Analysis, which breaks down complex signals into their fundamental frequency components.
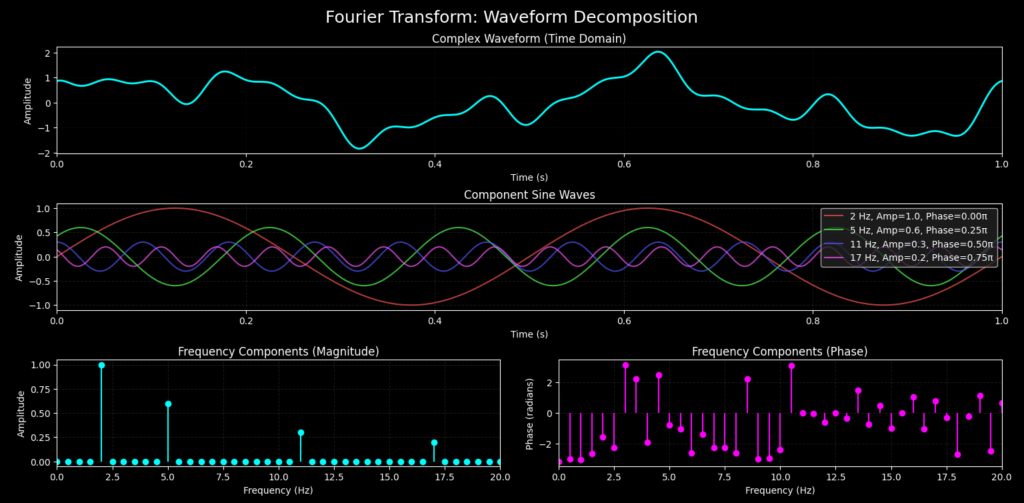
For example, in audio processing, a musical note played on a piano isn’t a single frequency but a combination of a fundamental tone and harmonics, each with varying amplitudes and phases. By analyzing these components, engineers can enhance, modify, or filter signals based on their desired properties.
Effects on Signal Transmission
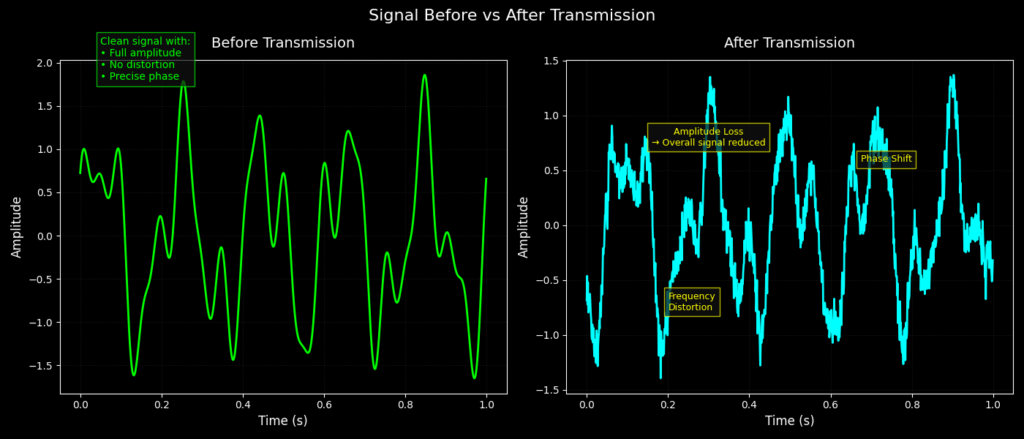
During signal transmission, frequency, amplitude, and phase interact with the medium they travel. This interaction can cause various distortions, affecting the signal quality and integrity.
- Amplitude Loss (Signal Attenuation):
As a signal travels over long distances, its amplitude decreases due to resistance, absorption, and scattering. This is a common issue in wired and wireless communication. For example, in fiber-optic cables, signals are periodically amplified to counteract attenuation.
- Frequency Distortion:
Different frequencies travel at different speeds depending on the medium, causing distortion. This effect is significant in telecommunications, where high-frequency signals may be more prone to loss than low-frequency ones.
- Phase Shift:
When a signal propagates through a medium, its phase can shift due to varying propagation speeds. This shift can cause synchronization issues in communication systems, especially in phase-sensitive applications like radar, GPS, and data transmission.
Practical Example: Audio Equalization
In an audio equalizer, the relationship between frequency, amplitude, and phase is actively manipulated to enhance sound quality. Equalizers adjust the amplitude of specific frequency bands while maintaining or shifting their phase.
- Increasing amplitude in a particular frequency range boosts those tones (e.g., increasing bass frequencies for a deeper sound).
- The adjusting phase can help prevent destructive interference in multi-speaker systems.
- Selecting specific frequencies allows filtering out unwanted noise, improving clarity.
This technique is widely used in music production, broadcasting, and live sound engineering to fine-tune audio signals.
Real-Life Example: Relationship in Circuit Design
In wireless communication systems, frequency, amplitude, and phase are altered for efficient data transmission. Different modulation methods change these properties.
- Amplitude Modulation (AM): The signal’s amplitude is varied while keeping frequency and phase constant.
- Frequency Modulation (FM): The frequency is varied while maintaining a constant amplitude.
- Phase Modulation (PM): The phase of the signal is changed to encode information.
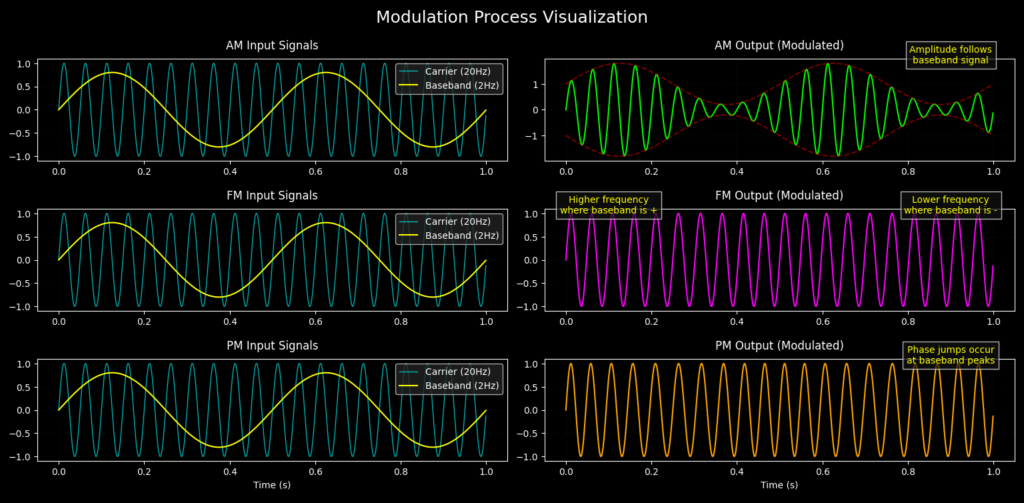
Each technique has its advantages and trade-offs depending on the application, such as AM radio, FM radio, and digital data transmission.
Similarly, filter circuits rely on frequency selection to allow or block signals of certain frequencies while preserving their amplitude and phase characteristics. A band-pass filter, for instance, is used in radio receivers to isolate the desired station while rejecting other frequencies.
Creator and Editor at AnitoCircuits.com based in Toronto
